最後更新日期 2024 / 01 / 01
CSS 動畫如何從中途開始播放
前言
事情是這樣的,前陣子在開發的網頁背景有個星空,於是就想說不如來加點星空的閃爍特效吧!
於是就先寫了這樣的 CSS:

不過這樣當然是不夠的,每個星星同時閃爍太不自然了,於是我加了一點隨機的 delay:
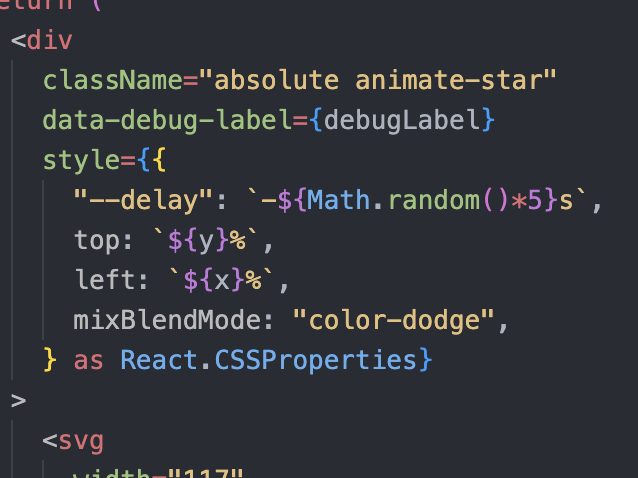
看起來是會隨機閃爍了,但在頁面剛載入進去的時候因為很多星星都還在 delay 中,畫面特別的空虛。這時候我就想了,有沒有可能讓 CSS 動畫從中途開始播放?
上網一查,原來還真的可以!
只要把 animation-delay 的值改成負數就行了!比如說 animation-delay: -3s 就是指從 3 秒開始的動畫。於是最後我把程式碼改成了這樣:
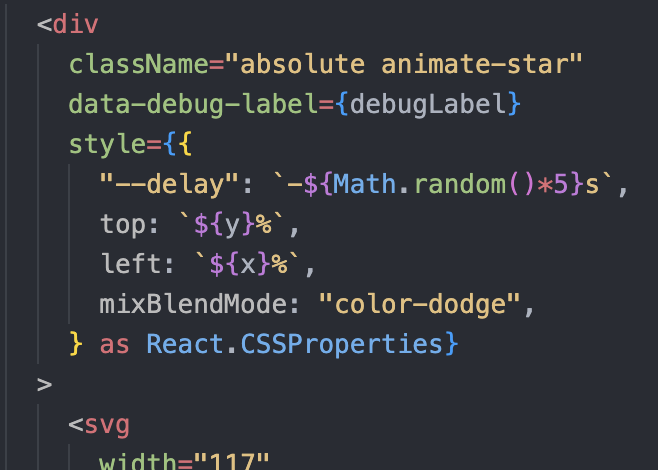
GIF 錄起來品質好像不是很好,但還是放一下好了

推薦文章
APCS 實作滿級完全攻略
筆者只是一個滿級的考生 以下內容都是根據個人經驗給出的建議考試名額不多 很快就會被搶完 所以開放報名第一時間記得趕快上去搶然後第一次應考前一定要先下載官方的虛擬環境 並且留意自己習慣的編輯器、IDE 有沒有在環境裡面 如果沒有的話就要事先練習好其他軟體的操作方式APCS 的實作題每次考試總共會有 4 題 每題 20 筆測資 每筆測資只要對了就可以獲得 5 分 所以就算沒辦法拿滿分 寫多少算多少 一定要傳上去- 基本程式語法如果只是要拿二級的話 其實練習方式還蠻廣的 基本上所有"會寫程式的人"都可以達到這個等級 也就是說 不管你想去寫網頁、開發遊戲、刷題目都應該可以達到 2 級這個目標- 二維陣列- 複雜模擬APCS 的 3 級範圍非常吃實作能力 需要邏輯清晰且可以處理複雜的操作才能達到 3 級 一個比較複雜的例子:APCS 202210 貨運站 而且在第二題當中 二維陣列操作出現的的頻率非常高 必須非常熟悉二維陣列 最後建議想達到 3 級分的話可以多練歷屆 APCS 第二題不過如果你的目標是更高的級分 其實不需要刷太多歷屆第二題 通常隨著能力提升實作能力也會自然提升- 排序- 搜尋- 貪心- 遞迴- 動態規劃- 資料結構4 級跟 5 級的範圍其實差不多 不過最大的差別就是要拿到 4 級只需要知道比較淺的知識就行了 那想達到 45 級的話就非常吃演算法和資料結構的運用能力 非常推薦這份 AP325 講義題目的部分 很常出現經典題或者經典題稍微改編 所以也很建議去 CSES 這個很多經典題的 Judge 多刷點題 可以配合 CSES 寶典 一起讀集結了多位 APCS 滿級分的出題者與驗題者 我們在每個月都會辦一場 APCS 模擬賽 如果還不清楚自己練習方向或想測試實力的話 歡迎加入 Discord 群組 重點是完全免費!!
APCS題解 CSES Trailing Zeros
n 階乘求數字有幾個後綴 0不難發現 後綴幾個 0 就等於乘進去的 10 的個數 而 10 = 5 times 2 所以後綴 0 數量就相當於計算把每個數質因數分解後 5 和 2 的較少的那個的個數 那當然 5 一定會比 2 少 所以我們要做的是就是計算 5 的個數 那要如何計算呢? 以 30 為例 我們知道要求得 30 階就是要把下面這些數字乘起來 不過我們可以先排除掉質因數分解後裡面沒有 5 的數字 然後把下面的數字都各取走一個質因數分解裡面的 5(相當於除與 5) 並把答案加上 6 因為下面有 6 個數字 變成這樣 可以看到下面的數字剛好就是 6 階乘的子問題 像剛剛的作法一樣 把跟 5 無關的數字排除並把它取走一個 5 的質因數 答案 += 1這樣就完成 30 階的計算了! 根據上面的操作 可以推出下列遞迴式 fx = flfloor frac nx rfloor + lfloor frac nx rfloor不過寫成程式其實用 while 迴圈就可以了 cppusing namespace std;signed main { int n; cin n; if n % 2 { cout 0 endl; return 0; } int ans = 0; while n = 5 { n = 5; ans += n; } cout ans endl;}
CSES題解 CSES Permutations
給予一個數字 n 你要使用數字 1 sim n 構造一個陣列 使得不存在任意兩個相鄰數字的差為 1把 n 個數字分成 1 sim lfloor frac{n}{2} rfloor 和 lfloor frac{n}{2}+1 rfloor sim n 兩堆 並穿插構造 ans 陣列就可以保證任兩數的差大約為 lfloorfrac{n}{2}rfloor 最後跑過整個陣列驗證是否合法即可cppusing namespace std;signed main { iosbase::syncwithstdiofalse;cin.tie0; int n; cin n; vectorint arrn; dequeint ans; int mid = n2; for int i = 1; i = n2; i ++ { int leftVal = i; int rightVal = mid + i; ans.pushbackrightVal; ans.pushbackleftVal; } if n 1 == 1 { ans.pushfrontmid + n2 +1; } for int i = 0; i n-1; i++ { if absansi+1 - ansi == 1 { cout "NO SOLUTION" endl; return 0 ; } } for int i = 0; i n; i ++ { cout ansi " "; } cout endl;}
CSES